那些跟高斯分布有些相似的概率分布【1】

这个系列打算跟大家讲讲一些概率分布，一些大家可能知道但又不那么了解的概率分布，这里我们不会像教科书那么样侧重具体的内容，而是希望大家从理解的角度去重新认识这些概率分布，因为深入的理解才会在你想要解决某一问题的时候想到这些看似无用的分布哦！

说到这个T分布，相信无论你是不是概率统计专业的学生，相信大多数一定是听过这个词语的吧！不过说句实话，其实这个Student-t Distribution想必对大多数的大多数来说是一个既熟悉又陌生的概率分布，说熟悉的是因为大概率的情况下，你知道对应的T检验并会使用查表来进行T检验，依稀记得这个分布似乎好像大概跟高斯分布有些类似，说陌生是因为大概率情况下你甚至都不一定可以快速写出其概率密度函数（pdf），甚至似乎好像大概可能这个这个pdf的大概图形在脑海中都不是那么的清晰。。。

嗯？啊？哦！是的吧。。。。那我们就来仔细看看这个分布吧！

Student-t Distribution的由来

在统计学上，这个分布与 Helmert，Lüroth 还有Pearson这些人名有关，不过这些科学家们的先后或许大家都不太在意，不过由于T分布更为大家津津乐道的故事就是这个“Student”这个名字的来由。这个Student的真名叫William Sealy Gosset， 然后就有各种版本的故事说到这个Gosset为什么要用Student啦，有的说这个是笔名，有点说就是为了匿名因为在他打工的啤酒产不允许他们发表文章，反正最终世人还是知道了这个Student背后的人，Gosset，当然之后让这个概率分布走向正式化的人，当然是一个牛人，Fisher！对就是那个 Ronald Fisher！

有兴趣的小伙伴可以去看看一些数学史的内容哈，毕竟这个不是我们这个系列的重点！

那重点是什么呢？

重点是Student-t distribution自身是如何被想出来的呢？

在之前的系列里面我们说到，高斯分布即正态分布，原先是在无聊投硬币实验中得到的分布的一个逼近，然后又是在误差分析中得到拉普拉斯与高斯的助力然后就成为了我们看到的高斯分布，当然Student-t distribution其实也有这样的故事！而它的故事来自于样本估计！

在我们大家熟知的基础版本的统计学中，其实最最最重要的就是两件事情，第一，参数估计（包括点估计与区间估计），第二，统计检验（即利用各种种类繁多的Test去统计学意义下考虑其相关性，同一性，相同性等等）。

这个我想请各位小伙伴回忆一下，最最最基础的参数估计，即高斯分布的期望与方差的估计。假设$X$ 来自高斯分布的随机变量（其均值为$\mu$, 方差是$\sigma^2$未知），这里对于均值的估计，毫无疑问，我们知道，

$$\overline{X}_n = \frac{X_1 + X_2, \cdots, X_n}{n} \tag{1}$$

这是样本的均值，并且这个样本均值可以用来估计总体这个来自高斯分布的随机变量$X$ 的总体均值$\mu$, 为什么呢？因为

$$\mathbb{E} \overline{X}_n = \mathbb{E} \frac{X_1 + X_2, \cdots, X_n}{n} = \mathbb{E} X = \mu$$

即用$\overline{X}_n$是一个无偏估计，所谓无偏估计即构成统计量在Expectation意义下与要估计的参数是一致的。

上面的式子说明一件事情，即总体的均值是可以被样本均值所无偏估计得到的呢？那么关于方差呢？首先总体的方差，即其定义

$$\sigma^2 = \frac{1}{m} \sum_{i=1}^m (X_i - \overline{X}_n) \tag{2}$$

其中m是总体的个数。那么对于在这个总体情况下，n个样本点所构成的样本的方差是否可以像均值那样给出总体的无偏估计呢？

答案是否定，因为此时我们要考虑的样本方差$S^2_n$（注意：样本的方差不等于样本方差）

$$S_n^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \overline{X}_n) \tag{3}$$

这里这个所谓的样本方差的虽然长得不太好看，但的的确确为了无偏，我们还不得不采用这个样本方差，至于从理解的角度看，为什么样本方差长成这个样子，这里有些非常不错的帖子，

为什么样本方差（sample variance）的分母是 n-1？ - 马同学的回答 - 知乎 https://www.zhihu.com/question/20099757/answer/312670291

为什么样本方差（sample variance）的分母是 n-1？ - 张英锋的回答 - 知乎 https://www.zhihu.com/question/20099757/answer/658048814

参考后面这篇文章的结论观点：即样本在估计过程中，由于是计算过程中引入的新信息（样本均值），让计算结果出现了偏差。为了让最终结果无偏差，因而需要对数据进行校正。原先$n$样本点在事实上是毫无约束的，即自由度为$n$,但是一旦计算了样本均值之后，并且在方差的计算中我们使用了这个样本均值当做总体均值，故对原先的样本进行的约束，即$n$的自由度现在只有$n-1$啦，这也就是为什$S^2_n$公式里面的分母是$n-1$的原因啦！

好啦，说了那么多与本文主题关系不大的内容，其核心就是想说到一个词语，自由度！下面从自由度角度，我们来看看这其中大家最为熟悉的统计检验部分，T检验。

Student-t Test与Z Test

在统计检验中，最最最基础的就是对于一个来自已知均值$\mu$与方差$\sigma^2$的高斯分布的随机变量，去检验该样本到底是不是来自于均值为$\mu$的总体，其$Z$统计量为

$$Z = \frac{\overline{X}_n - \mu}{\frac{\sigma}{\sqrt{n}}} \tag{4}$$

其中$\overline{X}_n$与$\sigma$分别来自于公式（1）与公式（2），同时我们得到的是这个Z统计量是需要来自于一个标准正态分布的！

Z检验被广泛使用在各个领域中，但是这里聪明的你自然可以发现一个存在的问题，即如果此时我们只知道其来自正态分布，但是并不知道其$\sigma$是什么值的时候，我们该怎么办？

由于之前我们说过，我们此时可以用样本方差$S_n^2$与近似替代$\sigma^2$,因此我们有个新的统计量，

$$T = \frac{\overline{X}_n - \mu}{\frac{S_n}{\sqrt{n}}} \tag{5}$$

由于在公式（4）中可以知道Z最后来可以服从的标准正态分布的，但是这个新构造的T现在显然就无法仍然满足正态分布的，因为毕竟$S_n^2$里面除以的是一个$n-1$，但是其实又没有太多的本质改变，直观来说，其实就是对原来分布进行一定程度上的伸缩！

当然最后，T检验的经验告诉我们，这个公式（5）给出的T其实就是服从来自于自由度为n-1的Student-t Distribution！

这里之所以说这个Student-t Distribution的自由度是n-1，其实就是因为这个$S_n^2$的表达式所造成的，其核心的核心原因，还是之前说的自由度，即这个$S_n^2$其实受制于$\overline{X}_n$，故而在自由程度上没有n个点的那么“自由”啦！

现在我们再来仔仔细细看看这个公式（4）与公式（5），既然后者到前者无非就是用样本方差$S_n^2$与近似替代$\sigma^2$，那么如果在Z与T的差别不就是直接取决于$S_n^2$与$\sigma^2$近似程度了么？

对哦！

那么什么时候$S_n^2$与$\sigma^2$差不多呢？什么时候差的很多呢？

考虑公式（2）与公式（3）以及些许极限的知识我们可以知道，当n很大很大的时候，大到样本都可以逼近总体的时候，那么自然$S_n^2$与$\sigma^2$算出来的结果不会差太远，相反，如果时这个n非常小，那必然除以n与除以n-1差距巨大啦！

所以的所以，是不是有一个我们熟悉的结论，即

学生t检验改进了Z检验（Z-test），因为Z检验以母体标准差已知为前提。虽然在样本数量大（超过30个）时，可以应用Z检验来求得近似值，但Z检验用在小样本会产生很大的误差，因此必须改用学生t检验以求准确。

原来如此！！！

Student-t Distribution究竟是什么？

好吧，说了不少内容，目前为主都是侧面描写哈，现在我们来看看这个Student-t Distribution到底是什么呢？

首先根据之前的侧面烘托，我们知道，

1. 这个是个概率分布！废话！当然啦！
2. 这个分布长的应该与高斯分布有些类似。这个也是的哈，毕竟乘以了不同的系数嘛！
3. 这个分布的当自由度趋向无穷的话，则可以趋向高斯分布！

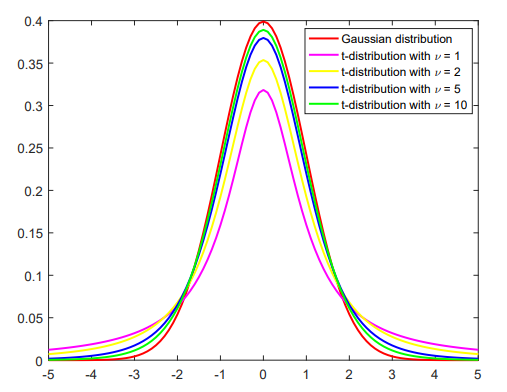
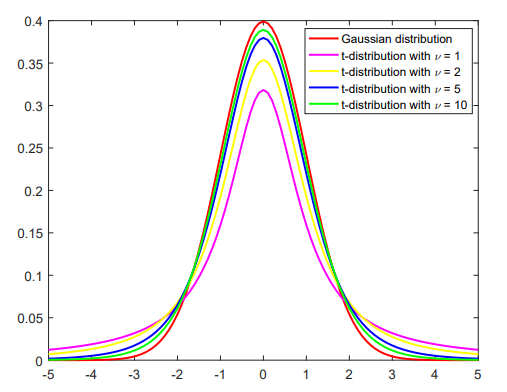
好啦，来看看这个Student-t distribution的庐山真面目吧！

这个图上也画出包括高斯分布在内的各种分布，其实$\nu$是自由度，直观来说，从中间看，高斯分布的尖尖头是在最上面的，而各类T分布则是好像被有人把这个高斯分布强行压下去的感觉，头被压下去，所以尾巴处就翘起来的哦！

因此，这类T分布很多时候也被视作Fat-tail distribution，即肥尾分布，当然现实中很多实际问题的刻画也更适合这种肥尾的分布而不非高斯分布，比如金融市场中，如果大家都按照正态分布来走，那么金融市场的风险就不会那么大喽！

好啦好啦，我们来看看最终的理论上的Student-t吧！当然其表达式看上去相对高斯分布来说那是复杂的太多了哈！

首先概率密度函数（pdf），

$$f(x) = \frac{\Gamma((\nu+1) / 2)}{\sqrt{\nu \pi} \Gamma(\nu / 2)\left(1+x^{2} / \nu\right)^{(\nu+1) / 2}}, \tag{6}$$

其中$\nu$自由度，$\Gamma$是伽玛函数。再看起累计密度函数（cdf）

$$F(x) = \frac{1}{2}+\frac{x \Gamma((\nu+1) / 2){2} F{1}\left(\frac{1}{2},(\nu+1) / 2 ; \frac{3}{2} ;-\frac{x^{2}}{\nu}\right)}{\sqrt{\pi \nu} \Gamma(\nu / 2)}， \tag{7}$$

其中$_2 F_1$是超几何函数。

额，好吧，这些东西实在太复杂了，记不住我也看不懂怎么办？

好吧，那就先让我们来看看这个千呼万唤始出来的Student-t distribution的一些特例吧！其中有不少概率分布界的大腕哦！

Student-t Distribution的两个特例

首先我们看一头一尾吧，头，当$\nu=1$的时候，其实这个T分布就退化成为了柯西分布， 即

$$F(x) = \frac{1}{2} + \frac{1}{\pi} \arctan(x)$$

$$f(x) = \frac{1}{\pi(1+x^2)}$$

尾，当$\nu=\infty$的时候，这时候其实T分布就是我们之前说的高斯分布啦！

这里直说要这两个T分布的极端的例子就想提前告诉大家一下，Student-t分布与这两个问题的关系匪浅，其实也就是意味着在下一节中介绍t分布的性质的时候，自然它将具体这两个分布类似的一些性质哦！

License

Copyright 2016-present 蓦风星吟.

Released under the MIT license.