时间序列和回归分析有什么本质区别？

如果说这个问题的本身：时间序列和回归分析有什么本质区别？

那回答一定是：

时间序列与回归分析根本不是一类东西！

不过在这里按照我之前做的一个课件的思路，希望可以大家厘清一些疑惑和误区。

什么是时间序列？

似乎听上去这个问题非常的蠢，很多人一定会说，我当然知道是时间序列啦，比如：

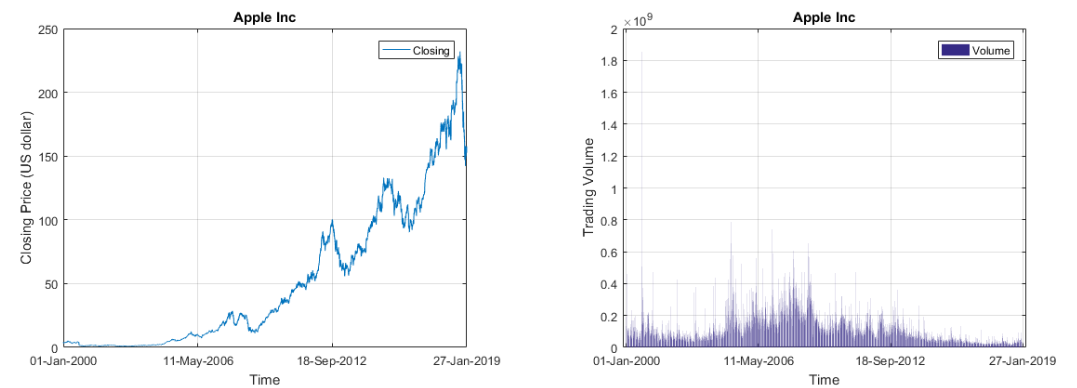
• 股票价格，成交量呀，这些都是时间序列呀！

• 日，月，季度，年的销售数据也是时间序列呀！

  

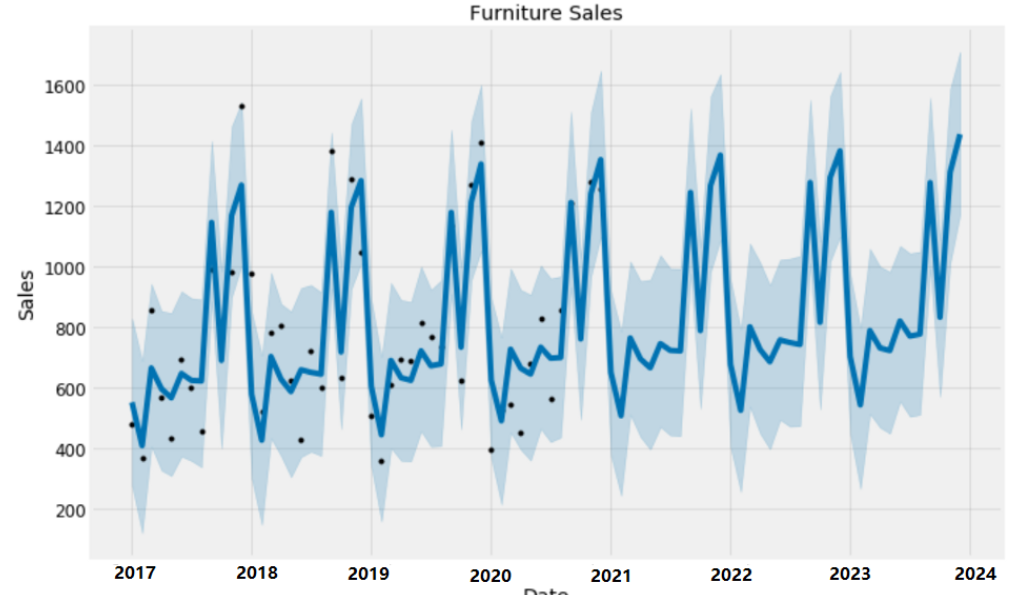
又比如基础扎实一些同学说说到，在XXX假设的提前下，我们得到的序列，用于分析YYY的方法就是时间序列呀！

没错，这些说的全都是对，但也不全对。其实没有什么复杂的，最最最简单的：

A time series is a series of data points indexed (or listed or graphed) in time order.

其实就是它的字面意思，indexed by time的series！所以最最最本质的内容，时间序列一种数据的类型，即一系列的点按照时间的顺序排排坐，至于“吃不吃果果”，这个就要看你啦！

如果你决定要“吃果果”，那么其实你在进行第二件事情，即：

时间序列分析！

什么是时间序列分析？

这其实也是极其朴素的问题，回答也应该极其朴素：

利用各种各样数学物理统计等等科学方法对时间序列进行分析，我们称之为时间序列分析。

紧着这个朴素的问题的应该会是个更加简单的问题：

“为什么我们要进行时间系列分析”，后者说换言之，“我们希望对时间序列分析后做什么呢？”

站在历史的长河中，其实可以用一个永恒的答案去回答：

• 了解过程
• 预测未来

作为人类，我们身处当下，但是总是希望可以了解我们的过去，了解这个世界的过去，同时我也希望可以预测自己的未来，预测这个世界的未来。

细节来说，了解过去，其实就是在finding important feature of historical pattern， 比如：

• 了解历史的走势，天下大势，合久必分，分久必合，大势所趋，等等
• 理解历史的周期，五年一个计划，60年一个甲子，500年一个轮回，等等
• 识别并记住那些重要时刻，比如各种朝代的更替与建立，比如那些历史高光时刻！

至于预测未来，其实就是在一件事情，构建历史与未来的连接，以便我们可以：

• 身处当下present，可以更好的去规划我们的未来
• 身处当下present，可以为我们未来的决策提供依据

或许你会觉得以上跟时间序列分析关系不大，不过我想说的是，其实关系非常大。别看“时间序列”无非是众多数据类型的一种，但是因为有“时间项”当然也正是有“时间项”，所以对它的分析就可以直接关联上我们的人类对于“了解过去，预测未来”的需求，通过时间序列分析，我们试图利用数学与统计的工具，定量的去刻画历史与未来的关系！

随机过程与时间序列分析

可能你会纳闷，我们不是正在讲时间序列么，为啥现在又出来个随机过程呢？

因为想要利用数学语言去规范我们要研究的对象，时间序列，最为适合的工具就是随机过程！

至于什么是随机过程，如果还是很困惑的小伙伴可以参考：

如何从深刻地理解随机过程的含义？ - 蓦风星吟的回答 - 知乎

可是为什么随机过程是最为合适的数学工具呢？

因为随机过程相较随机变量，它多一个虚拟的时间项！具体的解释可以在上面的回答中找到详细例子。

看看时间序列分析的对象，再看看随机过程的定义，看着应该还是挺适合的吧！

从概率统计的视角，用数学语言我们还可以将时间序列表述为：

A time series is a sequence of observations from a single process taken at a sequence of different times. In general, the notation ${x(t_i)}$with i = 1,2,···n is used to represent the sequence of n observations.

这里所说的single process指的就是一个单一时间index的随机过程。按照这个定义，其实时间序列本身是假定为来自一个随机过程的一组observation，对吧！

一起情况下诸多应用中都会考虑equally-spaced的时间序列，即：

Many applications typically involve observations taken at equally-spaced times and in this case it is usually written as ${x_t}$with t = 1,2,···.

既然是时间序列是来自随机过程的一组observation，那么它对应的随机过程是什么呢？

Time Series Process：时间序列过程！

The observed time series is modelled as a realisation of a sequence of random variable ${X_t}$ for t = 1,2,···n called the time series process.

这里需要强调的是，作为随机过程，time series process 是indexed在离散的时间域上并且其state space是连续的 （至于什么是stochastic process的index space与state space，请打开任意一本随机过程的教材）。

可是这是为什么呢？

这是因为虽然时间本身是连续的，但是事实上我们能够观测的却始终是离散个时刻，不过这个值却的的确确可以是视作是连续函数的函数值的哦！

敲黑板：

一般意义下，我们所说的Time Series时间序列，既指观测到的数据也指其对应的随机过程。

至于大家所提到的平稳性遍历性，其实是从其观测的数据所对应的随机过程的性质。

可是或许你会问为什么我们需要对其所对应的随机过程机型假设呢？

四个字： 简化问题！

当然更为确切的说是各种经典教材自然是从最初的最基础的最简单的开始讲啦！最简单自然是假设条件最强的啦！

举个例子来说，这个平稳性Stationarity，这是随机过程的里面极其重要的概念，因为它刻画了随机过程作为“一族”随机变量之间的关系，即相距一定时间距离的两个随机变量，他们的之间的相关性（协方差），而其中最常考虑的即是要求其固定， 即“弱平稳Weak Stationarity”也叫做“ 协方差平稳”。

再仔细往下思考，其实作为时间序列来说，这样对其对应的时间序列过程的假设其实具有非常强的合理性，因为我们的历史观让我们自然的去相信：

• 历史会重演
• 过去的经验可以被用来反映未来

其中最直接最简单的方式，就是去假设在过去60年一个甲子发生的事情，再未来60年一个甲子后也会发生！

表面上我们看到的是对数据的要求，而事实上其实这是对背后的随机过程的要求，即任意两个随机变量他们之间相关系的要求。

那么或许你还会好奇，如果没有平稳性，难道我们就不能研究时间序列（观测的序列以及随机过程）吗？

答案是显然的，自然可以啦！

比如经典时间序列分析中的ARIMA不就是nonstationary的process吗？

虽然本质也是stationary，因为只要I次差分就可以转化为stationary的问题了哦！

所以追根溯源核心还是目前我们有木有办法处理其对应的随机过程，若可以，自然对应的时间序列分析问题也是可以被解决的，比如从Markov的视角下，用递推去假设随机过程中随机变量的关系，也可以衍生出一系列的时间序列分析方法，只不过这些内容显然是超出了本科生的范围啦！当然如果有兴趣，可以参考一些非平稳时间序列分析的教材或者是论文哈！

什么是回归分析？

说了那么就的时间序列，时间序列分析，以及对应的时间序列过程，我们还是木有提到回归分析呢！别急，现在我们就来看看回归分析！

In statistical modelling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the ‘outcome’ or ‘response’ variable) and one or more independent variables (often called ‘predictors’, ‘covariates’, ‘explanatory variables’ or ‘features’).

查找关键词，我们可以知道，回归分析的核心是寻找自变量与因变量之间的关系，它是一系列的方法！

用数学一点的语言来说呢，其实就是考察以下表达式： $$ Y_i = f(X_i, \beta) + \epsilon_i $$ 其中$\beta$是模型的参数，$X$与$Y$分别代表着自变量(independent variable)与因变量(dependent variable)，以及$\epsilon$代表噪声。

当然我们的目标是去估计这个f的函数值，使得其尽可能的fit原来得出的数据

一般来说，想要去估计这个模型$f$， 参数化的思想下，我们至少要知道$f$的表达形式吧！比如线性模型，即$f(X_i, \beta) = \beta_0 + \beta_1 X_1$，然后我们再通过参数估计的方法去求出$\beta_0, \beta_1$即可，这里一般我们会考虑比如最小二乘，比如矩估计，比如极大似然估计等等。

不过总而言之的思路就是，给出模型形式，估计参数，获得模型！当然这里的前提是在一定的假设条件下。比如线性回归的假设，linearity， normality，iid。

某种意义下，这样的回归分析其实在做事情是：

假定自变量与因变量之间的关系，然后用统计工具去估计出其具体的量化关系。有这个这样的量化关系后，我们就是根据自变量与预测因变量啦！

举个例子来说，比如最广为人知的线性回归，linear regression，模型非常的简单，但是值得注意的是，在经典的教材中，为了方便后续的参数估计，一般我们会要求比如误差来自是正态分布，其均值为0，方差是常量。

那到底回归分析是不是一定要这些假设呢？

答案是显然的，不要！

在线性回归里面，除了linearity要求，其他都不是回归分析的要求，但的确是经典回归分析教材中的要求。其原因就是，有了这些假设，我们的参数估计，简便易算！因而如果你有兴趣，进一步去看看一些论文，就会发现有各种各样突破这些假设条件但仍然可以让模型work的方法哦！

当然，其实linearity条件也是可以突破的哦！

这就是非线性模型嘛！比如用高斯过程去做回归分析，则上述这些条件原则上都可以木有，有兴趣的小伙伴可以直接关注专栏：

高斯世界下的Machine Learning

话又说回来，既然回归分析是去估计自变量与因变量之间关系的方法，那么如果自变量是时间，不也应该是可以的吗？

对，没错！

因此，时间序列分析中的许多问题，也正是考虑的回归分析，比如多次被提到的AR模型。从名字autoregressive自回归我们就知道，这显然是一种特殊的回归，即今天的因变量是明天的自变量，一天一天往前滚。这种形式的回归非常符合时间序列数据的特点，因此也是被广泛考虑在时间分析中！

但由于其表达形式是线性回归的模型，那么自然需要考虑各种线性回归里面的假设条件了哦，并且基于此，已经有了一整套完整的理论体系啦！

但是是不是一定要如此呢？

答案是显然的， 不是！

因为你还可以考虑更加复杂的，只不过越简单的应用越广泛！

当然由于上面说到的线性回归之类的假设都是对数据点而言的，或者说是对数据点所来自的分布而言的，因而在多数情况下，在使用模型之前我们需要进行检验以确保或者说是一定程度上确保实际的数据点可以满足或者基本满足我们的模型假设！

比如test正态性，test独立性，test同方差异方差性，等等！这些内容会出现在回归分析中，当然也会出现在时间序列分析中有关回归的部分哦！

简单的小总结

时间序列分析：

研究对象：数据类型是时间的一系列数据点

研究目标：了解过去，预测未来

理论工具：随机过程

具体方法：回归（回归分析），分类，聚类等等

回归分析：

研究对象：具有因果（至少是数值上）关系的一组（多对一，一对多，多对多皆可）随机变量之间的数值关系！

研究目标：在给定假设的前提下（包括假定的模型形式），估计出相应的模型参数。

理论工具：参数估计

具体方法：各种参数估计方法，比如最小二乘，极大似然估计，矩估计等等

PS：事实上，回归分析也可以考察以下非参数的方法，那么后面就应该是跟着的是理论工具则是统计推断，具体方法则可以是各种非参数推断方法了哈！

时间序列数据的回归分析

在此之前看到许多小伙伴提到这个data science下的时间序列数据的回归问题，其中有一个个人觉得典型，即许多回归分析方法会利用未来的数据去预测！

其实这是个data science里面经常会遇到的问题，也是很多machine learning方法没有考虑到time series数据的实际特点所造成的问题。

如果你是做data science，那么自然不会陌生一些词语training, test, validation，许多时候我们不得不考虑使用validation set去避免模型的过拟合，后者用实际结果的语言来说就是，在training set上表现良好，但是在test上表现一塌糊涂的现象！

如何操作呢？

各种cross validation方法，比如Leave-one-out cross validation，比如K-fold等等。

那么这些具体的方法能不能被直接用在时间序列数据上呢？

答案是显然的，不能！

因为这就会发生用未来预测过去的情况，而这种情况是没有意义的！

那有没有什么方法是可以被用来做time series数据的cross validation的呢？

有！Rolling Windows也有的叫sliding windows但其实是一个意思，即利用cross validation的思想，但是在每一段的预测中都构造出对未来的预测来test模型结果！具体内容可以参考任意一本同时具有时间序列分析和机器学习的教材哦！